定量調査:
何人のユーザでテストすればよいか
ユーザビリティの計測を行うとき、20 人のユーザをテストすれば、大抵の場合は妥当な信頼区間を得られる。
ユーザビリティの質を表すには、ユーザの要する習得時間、効率、記憶量、犯す間違いの数、主観的な満足度など、品質指数として表現することが可能だ。残念ながら高い費用が必要になるため、そのような調査を行うプロジェクトは希だ。そういった調査には、簡単なユーザテストを行うのに比べて 4 倍ものユーザを必要とする。
各ユーザのパフォーマンスには大きな違いがあるため、より多くのユーザが必要となる。ユーザの計測を行えばどんな場合でも、とても速くタスクをこなす人と、とても時間をかける人が、多少いるものだ。それを考慮すると、ユーザの数を多くして、この差を緩和しなければいけなくなる。
ウェブユーザビリティのデータの標準偏差
過去に行った調査から、ウェブサイトでのユーザのパフォーマンスが正規分布になるということは、判っている。これは好都合だ。なぜなら統計で正規分布を扱うのは、容易だからだ。平均値と標準偏差の 2 つが判れば、そのデータの吊り鐘型曲線を導き出すことができる。
私は、幅広いウェブサイトとイントラネットで行った調査内で使用された 70 のタスクで採取した 1,520 の計測値を分析した。そこから導き出された標準偏差は平均値の 52 %だった。たとえばあるタスクにかかる時間が平均 10 分だったならば、その測定値の標準偏差は 5.2 分になるということだ。
例外の削除
標準偏差を計算するために、最初に例外的に著しく遅いユーザたちを取り除いた。これは、やってもよいことなのだろうか。状況によっては、やってはいけないことだ。遅いユーザというのは、現に存在する。そのため、デザインの品質を計測する場合は考慮しなければいけない。そのため統計分析では、例外的なユーザを省くことを勧めるが、彼らがいることを忘れてしまってはいけない。例外的なユーザには定性分析を行い、どのような「不運」(障害)が彼らのパフォーマンスを悪くしていたのかを見つけ出そう。
しかしながら、ほとんどの統計分析では、例外的なユーザを取り除いたほうがよい。なぜなら例外はランダムで起こるため、調査ごとにその数は上下し、そしてこれら少数の極端なデータが平均値などの結果に深刻なゆがみを生んでしまうことになるからだ。
統計値を出す唯一の目的は、他の統計値と比較するためだ。前述したような、タスクにかかった平均時間 10 分といった統計値は、それだけではあまり役に立たない。その 10 分というのはよいのか、悪いのか。その唯一の数値をスライドにして、独立した数字として感心しながら眺めたところで、何も見いだせないのだ。
電子メールのニュースレターに登録するタスクを調査した結果、平均時間が 10 分だったなら、それは著しく悪い。これは多くのニュースレター登録手順を調査した結果から、他のサイトでの平均時間が 4 分であるということと、ユーザが満足に感じるのは、その手続きにかかる時間が 2 分以下だった場合だけだということから、既に判っていることだ。それとは対照的に、ローンの申し込みといった、もっと複雑なタスクの場合、10 分という計測値はとてもよいユーザビリティを示していることになる。
重要なのは、ユーザビリティを計測するのは、自社サイトと競合サイト、または新しいデザインと古いデザインといった、他のユーザビリティの計測値と比べるためだということだ。
比較対象となる両方の統計値から、例外的なユーザを取りのいても、妥当な比較ができる。もちろん例外的なユーザを残していた場合は、どちらの統計値でも、タスクにかかった平均時間の値は多少高くなる。しかし例外を取り除いたほうが、正しい結果を導き出せる可能性が高い。なぜなら、そのほうが例外的なユーザたちの極端な平均値を過大評価してしまう可能性がなくなるからだ。
誤差範囲の予測
正規分布する観測値から平均を求める場合、その平均値の標準偏差は、個々の値から求めた標準偏差を観測数の平方根で割ったものとなる。たとえば、観測数が 10 であった場合、平均値の標準偏差は元の標準偏差の 0.316(10 の平方根)倍となる。
ウェブサイトとイントラネットのユーザテストでは、標準偏差が平均値の 52 %であることは判っている。言い方を変えれば、10 人のユーザをテストすれば、平均値の標準偏差は、0.316 × 0.52 = 0.16 であるため、平均の 16 %になるということだ。
たとえば、5 分かかるタスクをテストしているとする。この場合、平均値の標準偏差は 300 秒の 16 %になるため、48 秒ということになる。正規分布では、2/3 の場合は平均から± 1 標準偏差に収まることになる。したがって、平均は 5 分の平均値から 48 秒以内に 2/3 の確率で収まるということだ。
下のグラフは、信頼区間 90 %を求めていることを前提にした、様々なユーザ数でテストした場合で起きる誤差を示している(青い線)。これは、90 %の場合は許容範囲内に収まり、5 %の場合が低すぎて、5 %の場合が高すぎるということだ。実際のウェブのプロジェクトでは、これ以上正確である必要はない。
赤い曲線は、許容範囲を大きくして、正確性を 50 %まで落とした場合を示している。(つまり 1/4 の場合が高すぎて、1/4 の場合が低すぎてもよいとき。)
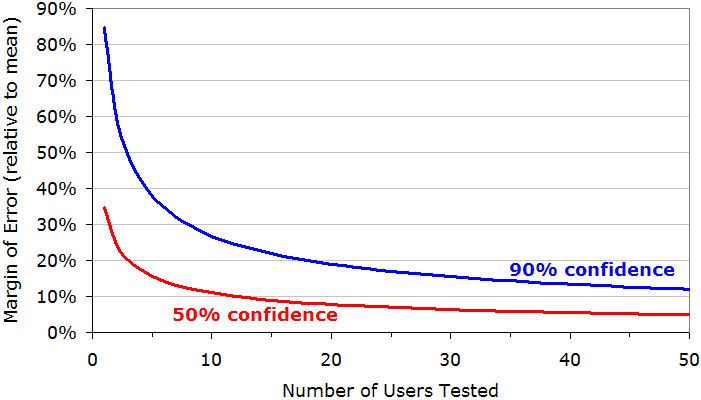
テストに参加するユーザの数
グラフ内で、誤差の範囲はユーザビリティ計測値の平均値の割合で示されている。たとえば、 10 人のユーザでテストしたとすれば、誤差の範囲は平均値の±27 %だ。これは、もしタスクにかかる平均時間が 300 秒( 5 分)ならば、誤差の範囲は± 81 秒ということになる。信頼区間は 219 秒から 381 秒の間になり、90 %の場合この区間に入り、5 %は 219 秒よりも低く、5 %の場合は 381 秒以上になる。
これは結構な幅のある信頼区間だ。そのため、私は通常ユーザ 20 人でテストすることを、定量的なユーザビリティ測定値を求めるときには勧めている。ユーザ数 20 人では、たぶん例外的なユーザが 1 人入る(全体の 6 %のユーザが例外的であるため)ことになるので、19 人のユーザのデータから平均値を出すことになる。19 人テストしたときの誤差は± 19 %になるので、これで信頼区間は 243 秒から 357 秒になる。
これでもなお信頼区間の幅がありすぎると思うかもしれないが、これ以上信頼区間を狭めるには、膨大な費用がかかってしまうというのが現実だ。誤差± 10 %を求めると、71 人のデータを必要とするため、5 人の例外的なユーザが混入することを考慮すると、76 人をテストする必要がある。
ほぼ全ての実際の開発プロジェクトにとって、 76 人ものユーザでテストするのは完全に金の無駄遣いだ。4 つの異なるデザインを各 20 人でテストすれば、許容範囲のデータが採取できるが、同じだけの予算を全て 1 つのデザインに集中させてテストしても、わずかに正確性の高いデータしか採取できないのだ。
実際、ほとんどの目的には、信頼区間± 19 %で十分だ。まず、2 つのデザインを比べて、どちらのほうがよい計測値を出すかを見るのが目的だ。そして、平均的なウェブサイトの差は 68 %であって、誤差の範囲よりも大きいのだ。
また、± 19 %というのも、最悪の場合だということを覚えておきたい。90 %の場合は、もっと正確な結果が出るだろう。赤い線は、ユーザ 20 人でテストを行い、19 人のデータを使った場合、半分の確率で ± 8 %の平均値内で収まることを示している。言い方を変えれば、半分の確率で素晴らしく正確な結果が出て、もう半分ではある程度正確な結果が出るということだ。学術的なプロジェクトでない限り、それで十分足りるのだ。
定量調査 対 定性調査
このような分析から、私は定量調査で 20 人でテストすることを勧める。テストユーザは、希少で、システマチックに募集して、ターゲット・ユーザを実際に代表できるような人材を集めなければいけないため、これにはとても高い費用がかかる。
幸運にも、ユーザビリティの改善のためには、それを計測する必要はない。普通は 片手で数えきれる数のユーザでテストして、彼らの行動を定性分析した結果から得られた指針にしたがい、デザインを改善すればよいのだ。何人か同じデザイン要素でつまずいても、どれほどユーザたちが時間を無駄にしているかを知る必要はない。ユーザの障害になっているのであれば、変えるか、削除すればよいだけだ。
一般的に定性調査は、ユーザ 5 人で済ますことができるため、定量調査は 4 倍の費用がかかることになる。さらに定量調査で間違いを犯すことによって、間違えた結果を導き出してしまうことも簡単だ。洞察でなく数字を集める場合、全てが正しく行われなければいけない。そうでなければ、やらないほうがマシなのだ。
高価で、正しく行うのが難しいため、普段は定量調査に警鐘を鳴らしている。ユーザビリティ調査を実施し始めて何回かは、定性調査であるべきだ。デザインの開発サイクルの中で統合されたユーザビリティを重んじるまでに、ユーザビリティが成熟し、定期的にユーザビリティ調査を実施するようになって、はじめて定量調査を何回か盛り込めるようになる。
記事で述べられている意見・見解は執筆者等のものであり、株式会社イードの公式な立場・方針を示すものではありません。


