定性的ユーザビリティ調査の数値が信用できない理由
定性的なユーザビリティ調査は、ユーザー数が少なく、プロトコルにばらつきがあるため、調査から得られる数値の測定誤差が大きくなり、母集団の実際の行動・態度を十分に反映していない可能性がある。
ユーザーデータを収集する最も一般的な方法の1つが、定性的なユーザビリティテストだろう。この方法では、通常、数人のユーザーを観察し、デザインの使いやすい要素や使いにくい要素を調べる。
リサーチャーの中には、定性調査でも、成功率(参加者がタスクを完了できたかどうか)やタスク時間、あるいは満足度やタスクの難易度、NPS、SUSなどの自己申告による指標などの数値データを収集することを好む人もいる。その結果として、レポートやプレゼンテーションでは、以下のような表現をよく目にする:
- ユーザーの70%がタスクを完了することができる。
- このデザインの新バージョンの使いやすさの評価は、旧デザインの評価よりもはるかに良い(6.2対5.1)。
- 平均満足度は7段階評価で6.7である。
しかし、これらの記述は誤解を招くものだ。その理由を理解するために、少し回り道をして、あらゆる測定の中心となる真の値理論について、まず考えてみよう。
真の値理論
デザインのユーザビリティを評価するには、ユーザー全体を対象とする指標の値を知りたいと思うことが多いだろう。たとえば、あるECサイトで、ターゲットとするユーザー全体の中で注文に成功した人の割合を知りたいとする。だが、(たとえば、小さな会社のイントラネットをデザインしているなどの理由で)オーディエンスが非常に少ない場合は別だが、何千人ものユーザーがいて、そうした数値を正確に測定することは不可能だ。結局のところ、その計算をするには、一人一人のオーディエンスにサイトでもれなく注文をしてもらい、彼らの注文が成功したかどうかを記録する必要があるからだ。
この母集団全体に基づく指標の値を真の値(true score)と呼ぶ。しかし、この値は正確には測定できないものである。ただし、推定することは可能だ。これがまさにユーザーのサンプルで調査を実施し、参加者に注文をしてもらうということにあたる。この調査から得られるのが測定値(サンプル中、何人のユーザーがタスクを完了できたか)である。この測定値は、真の値を予測するためによく利用される。
しかしながら、測定値は真の値と同じではない。真の値理論では、両者は測定誤差によって異なるとされている:
測定値=真の値+測定誤差
測定誤差が小さい場合、測定値は真の値の良い予測になる。しかし、誤差が大きければ、測定値は真の値についてあまり多くのことを伝えてはくれないだろう。
小さなサンプルサイズ、大きな測定誤差
経験則として、調査のサンプルサイズが小さいと、測定誤差は大きくなる。この理由を理解するには、調査の参加者はそれぞれ自分の個人的なコンテキストを調査に持ち込むということを思い出すとよい。eコマースに精通していて、オンラインでの買い物にほとんど苦労しない人もいれば、体調を少し崩していて、タスクに集中するために努力が必要な人がいる可能性もあるし、調査のファシリテーターのことを気に入って、彼らを喜ばせるために最善を尽くす人もいるかもしれない。こうした個人的なコンテキストはノイズといえる。デザインの品質とは何の関係もないのに、測定値に影響を与えるからだ。調査結果を何らかの形で歪ませかねないということだ。たとえば、気が散っている人は、サイトでのパフォーマンスが低下して、タスク時間が長引き、エラーも増えて、満足度が下がるだろう。(あるいは、楽しく調査に取り組む意欲的な参加者は、現実よりも良いスコアを出してしまう可能性がある)
調査の参加者がごくわずかである場合(たとえば、5人とか10人)、彼らの個人的なコンテキストが調査結果を歪める可能性は非常に高い。しかし、多くの参加者を対象とする調査では、個人的なコンテキストは相殺される。つまり、不満があり、悪い評価をする人がいれば、楽しく調査に参加して、良い評価をしてくれる人もいるのが普通だ。
したがって、調査対象者の数が少ない場合、調査から得られる推定値は、そのユーザーグループ全体で起こることの適切な予測にはならない。ノイズがデータ内のシグナルを圧倒する可能性が高いからである。
統計はその数値が信頼できるかどうかを教えてくれる
サンプルサイズは、数値を信頼できるかどうかを知るための良いヒューリスティックとなるが、もっと良い方法がある。実際のところ、統計を使えば、調査の測定誤差を正確に推定することができる。
調査から得られた1つまたは複数の数値が真の値の予測として適切であるかどうかを示す統計的な手段には、信頼区間と統計的有意性の2つがある。
信頼区間
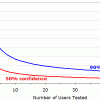
信頼区間は、調査で測定された数値が真の値をどの程度予測しているかを定量化するための統計的手段である。信頼区間は、真の値である可能性が高い範囲、言ってみれば、真の値が測定値とどの程度異なると考えられるかを示す。たとえば、100人の参加者のうちの50人がタスクに成功した調査から、母集団全体の成功率の信頼区間を計算すると、40%から60%となる。言い換えると、真の成功率は40%から60%の間のどこかということであり、それは42%かもしれないし、59%の可能性もある。また、真の値は50%±10%であるともいえる。すなわち、この調査の測定誤差は±10%である。(この記事で計算された信頼区間はすべて、本当の95%信頼区間である。しかし、この記事の目的からすると、信頼度は専門的な情報なので、あえて主張することはしない)
信頼区間は、サンプルサイズに強く影響される。たとえば、10人のユーザーで調査を実施し、そのうちの5人がタスクを完了した場合、信頼区間は50%±26%、すなわち24%から76%になる。つまり、成功率がそこそこ良い場合には75%かもしれないし、非常に悪いと32%のこともありうる。このようにユーザー数が少ないと、測定誤差は大きいし、推定される範囲も非常に広い。
しかし、100人のユーザーを調査対象にして、そのうちの50人がタスクを完了したとすると、測定値は50%のままだが、信頼区間は50%±10%(または、40%から60%)となり、測定誤差ははるかに小さくなる。
統計的有意性
信頼区間は、測定値に基づいて真の値の範囲を説明するために使われる。それに対して、統計的有意性は、2つの測定値を比較できるようにするものだ。統計的有意性は、2つの測定値の差異が、対応する真の値間の本当の差異を反映している可能性が高いか、それとも単なる偶然によるものなのかを教えてくれる。
AとBという2つのデザインについての調査を行ったところ、AとBの成功率はそれぞれ60%と70%で、デザインBはデザインAよりも優れていることを示唆する結果が得られたとしよう。しかし、これらの数値は測定値であるため、ノイズが含まれている。したがって、2つのデザイン間の10%という測定値の差異は実際の差異を反映していないとも考えられる。言い換えると、デザインAの真の成功率は65%、デザインBの真の成功率は60%で、実際にはデザインAのほうがはデザインBよりも優れているという可能性もある。
統計的有意性を使えば、測定された差異が実際のものなのか、単に測定ノイズの影響なのかを知ることができる。統計的有意性の検定には、さまざまな状況に適したいろいろな種類があるが、それらはどれもp値(差がデータの偶然性やノイズに起因する確率)を返す。p値が小さければ(0.05未満)、その差は統計的に有意であるといえる。つまり、真の値の実際の差異を反映しているということだ。
先ほどの例に戻ると、統計的有意性の検定を行わない限り、単に測定値だけでデザインBがAよりも優れているかどうかを断定することはできない。我々はその差が統計的に有意であるかどうかを調べる必要がある。そして、その差が統計的に有意である場合にのみ、デザインBはデザインAよりも優れているということができる。
定性調査におけるプロトコルのばらつき
ここまでの話で、調査の規模が小さいと、一般的には大きな測定誤差が生じるということを納得していただけたと思う。これが、定性調査での成功率が70%であろうと20%であろうとそれほど意味はなく、小規模な調査で母集団全体に適用できる推論を行うことが難しいことの最大の理由である。
しかしながら、定性調査の数値が信頼できない理由はさらにある。それが調査プロトコルのばらつきだ。
定量的なユーザビリティテストでは、測定誤差に影響を与える交絡変数(編注:「結果変数」とそれを説明する「独立変数」の両方に相関する変数)が加わっていないことを確認するために、リサーチャーは内的・外的妥当性の確立に努める。定量テストでは、通常、調査条件が厳密に文書化されており、参加者ごとにそうした仕様に忠実に従う。対面の定量調査であっても、一般にモデレーターの介入はほとんどない。
対照的に、定性的な調査は、多くの場合、形成的な性質をもつ。つまり、デザイン上の問題を特定し、できるだけ早く修正することを目的としている。定量調査とは異なり、定性調査では、ファシリテーターが明確化のための質問をしたり、(願わくばプライミングをすることなく)興味のある方向に参加者をある程度誘導できる自由度がある。たとえば、パラレルテストや反復テストをおこなっている場合などには、セッションごとに異なるタスク、あるいは異なるデザインをテストすることさえある。
その結果、定性的なセッションは、次のセッションとは同じでないことが非常に多い。ファシリテーターの介入度が異なることもあれば、参加者が思考発話で言語化する度合いが違う場合もあるし、ときにはタスクやインターフェイスまで変わることもあるからだ。このようなプロトコルのばらつきは、結果的にはデータのノイズを増やすことになる。あるサイトで何の助けも借りずにタスクを完了した参加者もいれば、ファシリテーターの助言を繰り返し必要とした人もいたとしよう。彼らの成功率やさらには満足度も最終的には同じだったが、それはひとえに外的な要因によるものと考えられる。
このような流動性こそが定性テストの強みであり、定性テストがデザインの問題点をすばやく特定するための素晴らしいツールである要因だ。しかし、このことは定量的なテストよりも定性的なテストのほうがノイズの多い数値が出やすい理由の1つでもある。
統計解析なしの数値を報告してはならない
一般に、母集団のサンプルに基づいて数値を報告する場合は、計算が必要だ。つまり、信頼区間や統計的有意性を計算して、測定値(調査で得られた数値)が対応する真の値や母集団全体の行動・態度をどの程度予測できるかを確認しなければならない。
このルールには、例外が1つだけある。それはサンプルの対象が母集団全体である場合だ。その場合は一切予測をすることはない。単に真の値を報告するだけだ。たとえば、自分の高校の100人いるクラスで、青い目の人の割合を知りたい場合は、単に人数を数えて、割合を報告するだけである。信頼区間は必要ないからだ。しかし、NNgroup.comの記事の読者のうちの青い目の人の割合を知りたい場合、それを数えるのは無理だろう。サンプルを取り、そのサンプルのうちの何人が青い目をしているかを確認して、そのサンプルに基づいて信頼区間を計算し、それを青い目の読者の割合の予測される範囲として報告しなければならない。
ステークホルダーが小規模の調査の結果の数値を見たがる場合は、その数値を正しく提示してから、それが信頼できないことを明確にするとよい。今回の結果が母集団全体に一般化されるかどうかについても必ず言及しよう。今回の調査のみに当てはまるように注意深く文章化したところで、人というのは一般化してしまうものだからだ。たとえば、「今回の調査の平均満足度は7段階評価で6.7だった」と書いたとしても、ステークホルダーは、「自社の全ユーザーの平均満足度評価は6.7である」と受け止める可能性が高い。したがって、母集団全体について推論できることがあるかどうかについては常に明示的に記載する必要がある。
| 不適切な報告 | 適切な報告 |
|---|---|
| ユーザーの70%がタスクを完了することができる。 | この調査の参加者のうち、70%(10人中7人)がタスクを完了した。この結果から、母集団全体での成功率は39%から90%(95%信頼区間)であると推定される。 |
| このデザインの新バージョンの使いやすさの評価は、旧デザインの評価よりもはるかに良い(6.2対5.1)。 | 今回の調査では、このデザインの新バージョンの使いやすさの評価が旧デザインよりも高かったが、この差はp > 0.05で統計的に有意ではなく、母集団で再現される可能性は低いと考えられる。 または、p < 0.05の場合: このデザインの新バージョンの使いやすさの評価は、旧デザインよりも高く、この差はp < 0.05で統計的に有意だった。 |
| 平均満足度は7段階評価(1=低い、7=高い)で6.7である。 | 今回調査の平均満足度は、7段階評価(1=低い、7=高い)で、6.7だった。母集団全体の平均満足度は5.2から7(95%信頼区間)になると予想される。 |
結論
どんな調査も、対象がユーザーのサンプルのみである場合には測定誤差が生じる。ほんのわずかな参加者を対象とする調査から得られた数値は、通常、大きな測定誤差をもたらし、予測の判断材料にするには不十分だ。測定誤差の大きさや、調査で得られた数値が母集団全体の行動・態度をどの程度予測しているかを理解するには、信頼区間や統計的有意性などの統計的手段を利用する必要がある。
記事で述べられている意見・見解は執筆者等のものであり、株式会社イードの公式な立場・方針を示すものではありません。