統計的有意性の理解

※「定量分析の危険性」への補足記事

本文で私は、統計分析だけに頼ると「有意とされた結果のうち、1/20 はランダムである可能性がある」と書いた。これはちょっと簡略化しすぎた言い方だ。詳細はこうだ。

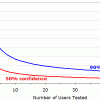
「統計的な有意性」はその結果が、もし本当に何も理由がない場合において、その現象がランダムで起きる確率を示す有意水準に依存している。この有意水準は「p」として表記され、有意性を認めるのにpは一般的に 5％より少ないことが求められる。研究者は、広い分野に大きな影響のあることに対しては、さらに強い有意性を求めて、pが 1％、さらには 0.1％よりも少ないことを求める。

本当に何も相関性がない質問を 20個用意して実験を行い、相関分析を行うと、平均して 1つの相関関係が「有意」だと出ると予測される。これは発表されている研究の 1/20 が間違っているという意味ではない。もし、対象となる問題についての理解抜きに調査を設計し、結果だけをあさるならば、統計調査の20に1つは間違っているということだ。

良い研究者は、定性的な洞察をもとに仮説を立てることからはじめる。たとえば、人がどのようにオンライン上で読むかを観察したあと、流し読みに適したレイアウトが、ウェブサイトの内容を簡単に読み、理解することを可能にしているのではないかと考える。もし統計的な調査を、真実ではないかと思われる疑問に行えば、間違えた結果が出るとはあまり考えられない。

ひとつ思考実験をしてみよう。ある研究者 Bob 博士が100の仮説を立て、そのうちの80％が真実だとしよう。例の統計分析にしたがえば、Bob は間違った20の仮説のうちのひとつを、誤って信じ込んでいることになる。Bob が、充分な統計的裏づけのある調査を行ったとしよう。彼は、真実である80件の仮説のほとんどを受け入れ、10件は重要性を認めずに無視する。Bob はその後に結論として71件を公表するが、このうちの70件は真で、1件は偽である。言い換えると、Bob の論文のうちで、デタラメといえるのはわずか 1.4％でしかないのだ。

残念ながら、実世界の研究者の全員が、正しい仮説を80％の確率で導き出せるほど優秀とはいえない。また、あらゆる調査が、80の正しい仮説のうち、70件を受け入れられるほどの統計的裏付けを持つわけではない。したがって、発表されている定性調査の中にある、間違いの割合はもっと高い。しかし、その割合は、研究者の能力と先行研究の洞察に依存するため、計算して出せるものではない。