フィッツの法則と、UXにおけるその応用
ターゲットまでの移動時間は、ターゲットの大きさとターゲットまでの距離に依存する。
歴史
ポール・フィッツは、ヒューマンエラーが単なる人間による誤りではなく、不適切なデザインに起因することを理解した最初の心理学者の1人である。彼は第二次世界大戦中に飛行機のコックピットのデザインを研究し、ヒューマンエラーが原因であるとされていた多数の戦死が、実際にはデザインの不適切さによるものであると主張した。
1950年代になると、彼はシャノンの有名な情報理論の影響を受ける。そして、ジョージ・ミラーがチャネル容量の概念を人間の記憶に適用し、その過程で人間の短期記憶の情報処理能力として有名なマジカルナンバー7を導き出したように、フィッツは人間の動作能力、つまり、人が一定の時間内に何回の反復運動をすることができるかを調べようとした。彼はそのような反復運動を含むいくつかの実験を行い、その結果、ヒューマン-コンピュータインタラクションに関するもっとも有名な法則の1つであるフィッツの法則を導き出したのである。
フィッツの法則
フィッツの法則は、ポインター(マウスカーソル、人間の指、手など)が特定のターゲット(物理的またはデジタルのボタン、物理的なオブジェクトなど)に移動して、何らかの方法でそのターゲットとインタラクトする(クリックする、タップする、握るなど)のにかかる時間(T)についての関係性を示したものである:
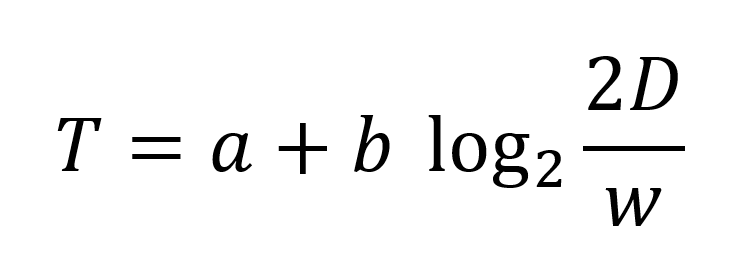
ここでは、Dはターゲットまでの距離、wはターゲットの幅(厳密には、移動軸基準での幅)、aとbはポインターの種類(マウス、指など)によって異なる定数である。
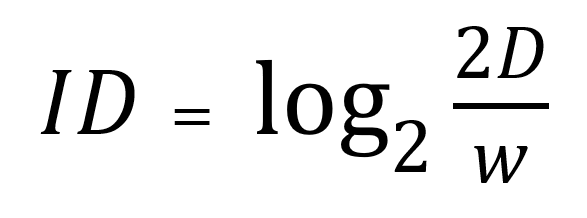
上の式は難易度指標(index of difficulty)とも呼ばれ、単位はビットである。したがって、フィッツの法則は以下のようにも表せる:
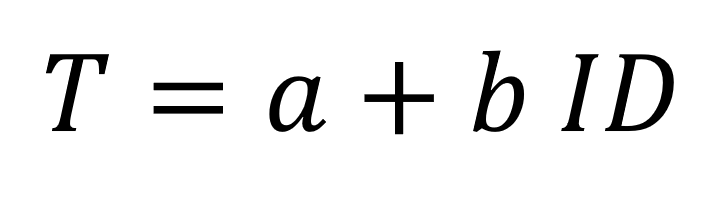
厳密に言うと、フィッツの法則の方程式では、移動方向からみたターゲットの幅が用いられる。しかし、ユーザーインタフェースで一般的な長方形のターゲットの場合、この値はターゲットの寸法のうちの高さか幅のどちらか小さいほうに置き換えることができる(1992年にScott MacKenzieとBill Buxtonによって証明された)。
この数式がわかりにくいと感じる人は、以下の2つの文がこの式の主旨である:
- ターゲットまで距離が遠いほど、ポインターがターゲットに移動するのに時間がかかる。言いかえると、近くにあるターゲットはより早く捕捉できる。
- ターゲットが大きいほど、ターゲットまでの移動時間は短くなる。言いかえると、ターゲットは大きいほどよい。
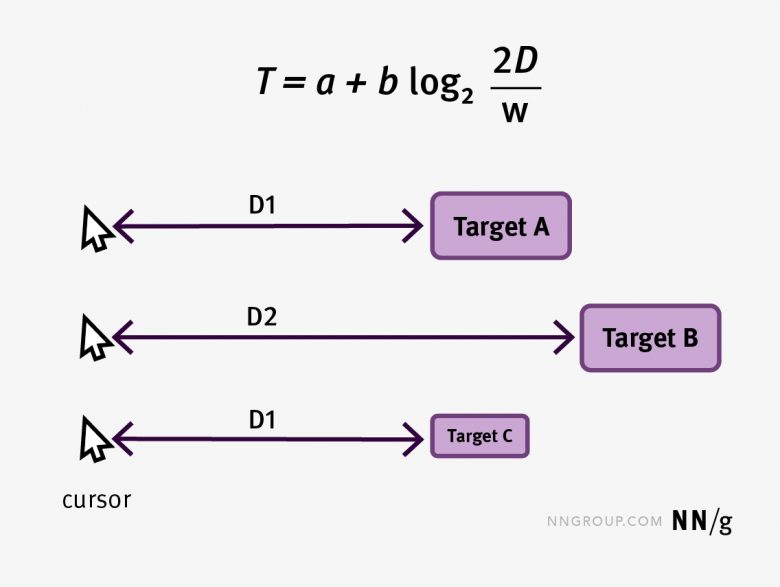
この方程式には対数が含まれている。つまり、移動時間はパラメータに対して直線的に伸びるのではなく、その伸び方はよりゆっくりとしたペースになる。したがって、2倍離れたところにあるものへの到達時間はもっと長くかかるが、2倍ではない。なぜならば、移動というのはまず加速し、その後、減速するものだからだ(次のセクションで説明)。これは距離が長くなると、移動時間中にポインターを移動させるスピードも速くなり、その結果、ターゲットに近づくと、より多くスピードを落とす必要があるということを意味する。
まさにこれが以下で説明する2成分モデルの本質である。
2成分モデル
フィッツよりずっと前の19世紀末、人間の身体運動の研究の先駆者の1人であるR. S. Woodworthは、上肢の動きについての2成分モデルを発表した。このモデルによると、目標に向かう動き(たとえば、音楽のリズムに合わせて拍子をとるのではなく、ターゲットをとらえるために実行される動き)は、2つの成分に分解することができる(これがモデル名の由来である):
- ポインターをターゲットに向けて動かすための高速で比較的粗い初期動作。
- 精度を確保する(たとえば、ターゲットを正確にとらえる)ためのゆっくりとした最終動作。
第1段階は、ターゲットまでの距離に大きく左右される。この動きの目的はポインターをできるだけ早くターゲットに向かわせることにあるからだ。一方、移動の第2段階は、主にターゲットの大きさに左右される。ターゲットを行き過ぎたところをクリックしないよう、ポインターの速度を下げる必要があるということだ。ターゲットが小さくなればなるほど、この第2段階に費やされる時間は長くかかる傾向にある。
UXへの応用
フィッツの法則が持つ意味は、移動時間に影響を及ぼす2つの変数(ターゲットの大きさとターゲットまでの距離)にそれぞれ相当する、2つのカテゴリーに分けて考えることができる。
ターゲットの大きさの最適化
大きいほどよい
フィッツの法則から得られる示唆としてもっともわかりやすいのは、ターゲットを大きくしよう、ということだ。フィッツの法則によると、ターゲットが大きければ、ターゲットのクリックやタップ、マウスオーバーをより早くできることが明らかだからだ。それだけでなく、ターゲットが大きくなればエラー率も低下する。一般に、ターゲットの大きさのガイドラインは、さまざまな大きさのターゲットに関してエラー率を取得してから、エラー率が横ばいになる大きさを特定することで作成することができる。
アイコンにはラベルを
アイコンにはラベルが必要だと我々はこれまで何度も言ってきた。テキストラベルはアイコンのあいまいさを減らしてわかりやすくするだけでなく、その特定のターゲットへの移動時間も短縮するからである。それはなぜか。単純な話だ。アイコンとラベルの両方で構成されるターゲットのほうが単なるアイコンよりも面積が大きくなるため、フィッツの法則がいうように、捕捉しやすいからだ。(もちろんこれは、アイコンのみをアクティブなターゲットにするというデザインミスをせず、該当のエリア全体をクリック可能にしていることが前提である)

画面端に沿って配置される無限大のターゲット
この2成分モデルでは、ターゲットが非常に大きい場合、あるいは無限大であれば、最終動作という成分をかなり小さくすることができる。ターゲットが無限大であれば、ポインターの移動をどこで止めるかが問題にならないので、ターゲットに対して行き過ぎる心配がないからだ(もちろんこれは、ポインターがターゲットエリアにすでに到達していることが前提条件である)。
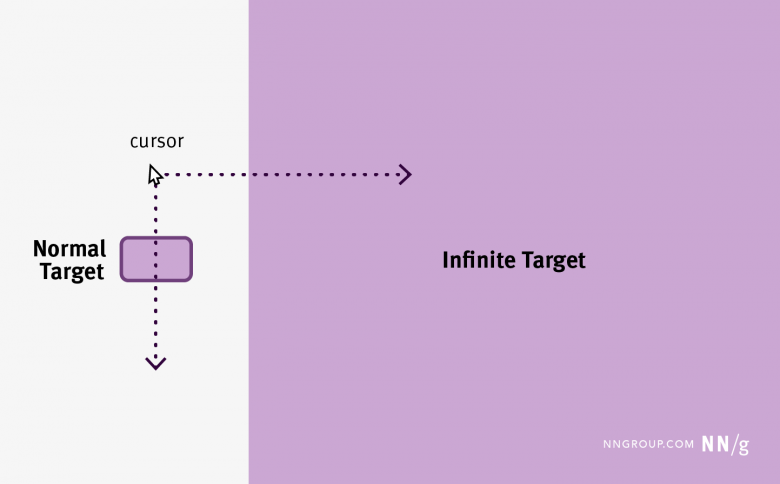
ここで、実際のインタフェースデザインのどこに無限大のターゲットがあるのか、と疑問に思う人もいるだろう。その答えは、インタラクションがマウスを使うものであれば、画面の端である。実際、画面の端はカーソルにとっての自然な壁として機能する。ポインターは端に到達すると、その壁にぶつかったときの速度に関係なく、そこから先には行けないからである。
したがって、より正確にいうと、到達するターゲットが画面の端にある場合、ターゲットが画面の中央にあるときのようにユーザーは減速しなくてよい。なぜなら、行き過ぎる心配がないからだ。ポインターは画面の端に当たると自動的に動かなくなるからである。
オペレーティングシステムのデザイナーは、フィッツの法則から導き出されるこの結果をうまく活用している。MacOSでは、アプリケーションメニューは画面の水平方向の最上端に表示されているので、ユーザーはこのエリアに非常に楽に到達することができる。Windowsでも(少なくともWindows 8までは)、スタートボタンは画面の左下隅に配置されていた。どちらのオペレーティングシステムでも、頻繁に使うさまざまなアプリケーションのアイコンは画面の最下部に並べられている。
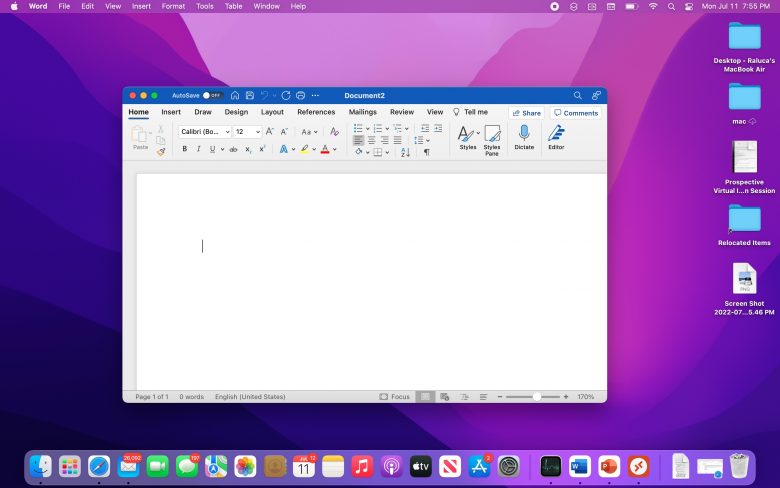
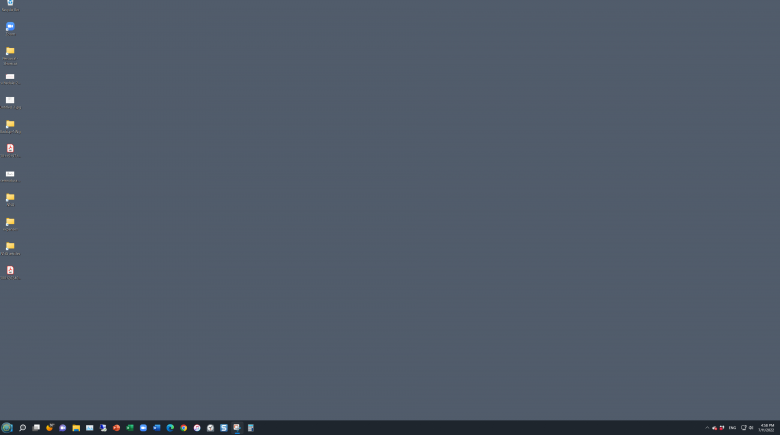
ただし、端部分へのこうした配置はマウスやトラックボールで操作するUIにはメリットがあるが、タッチスクリーンの場合は何の利点ももたらさないことに注意しよう。実際、Daniel Avrahamiの研究によると、タッチスクリーンデバイスでは、ターゲットを端部分に配置すると、ヒットするのに実際には時間がかかるようになることがわかっている。タッチスクリーンでは、ターゲットを行き過ぎてしまって、画面の端を越えたところをヒットしてしまう可能性があるためではないかと考えられる。
ターゲットを密集させてはならない
ターゲット同士を近づけすぎると、ユーザーが誤ってターゲットを行き過ぎてしまって、間違ったターゲットを起動させるリスクがある。特に、ターゲットが小さいとこうしたことが起こりやすいので注意しよう。
パディングだけでは不十分
デザイナーの中には特定のターゲットにパディングを入れて、有効なターゲットエリアを増やそうとする人もいる。パディングはターゲットを行き過ぎてしまうことによるエラーをある程度防ぐことはできる。ただし、ターゲットがパディングされていることにユーザーがまったく気づいていない場合、ターゲットエリアを超えないように彼らがターゲットに近づくにつれて慎重になり、必要以上に減速してしまう可能性があることを覚えておこう。
ターゲットまでの距離の最適化
メニューのデザイン
項目のリストを表示するためのメニューの種類は、メニュー内のそれぞれの項目への移動時間に影響する。その理由を理解するために、リニアメニュー、レクタングルメニュー(別名メガメニュー)、パイメニューという3種類のメニューについて考えてみよう:
ここでは、メニューが開かれたとき、ポインターはメニューハンドルまたはラベルの上にあるとする。(これは、マウスベースのインタフェースでは現実的な仮定といえる。キーボードのアクセスキーによってメニューを開くこともなくはないだろうが、マウスを使ってメニューを開くほうがシナリオとしてはより一般的と考えられるからだ)。
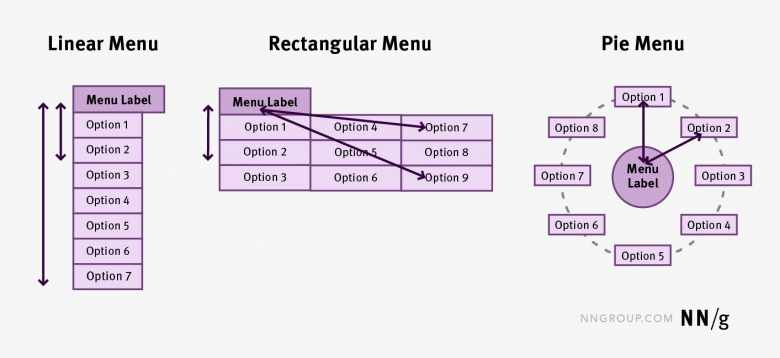
リニアメニューでは、メニューハンドルからメニューの最初の要素までの距離がもっとも短く、メニューの最後の要素までの距離がもっとも長い。したがって、このメニューでは、使用頻度によって項目を並べる(アクセス頻度がもっとも高い項目を一番上に持ってくる)ことを検討するとよい。
レクタングルメニューでは、水平方向と垂直方向に項目が整列している。結果として、メニューの選択肢までの平均距離は、メニューを直線的に並べる場合よりも近くなる。
最後に、パイメニューでは、すべてのメニュー要素がメニューハンドルを中心とした円周上に配置されるため、各要素のハンドルからの距離は等しいものになる。その結果、各選択肢に到達するまでの時間も同じになる。(パイメニューはこのように大きな利点があるにもかかわらず、UIデザインではまだ他のメニューほど使われていないため、ユーザーには馴染みが薄い)。
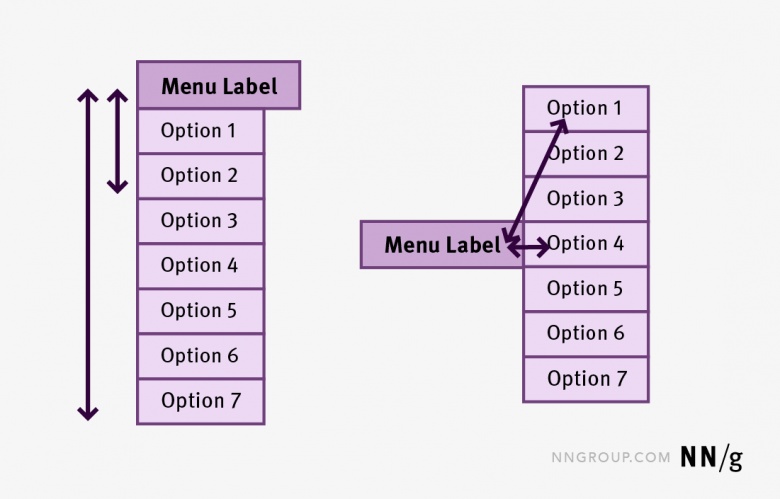
簡素なリニアメニューであっても、すべての要素に比較的均等にアクセスがある場合は、ハンドルをメニューの真ん中に合わせて配置すれば、もっとも遠くにある要素が最初と最後の項目、もっとも近くにある要素が中央の項目ということになるので、平均移動時間を短縮することができる。
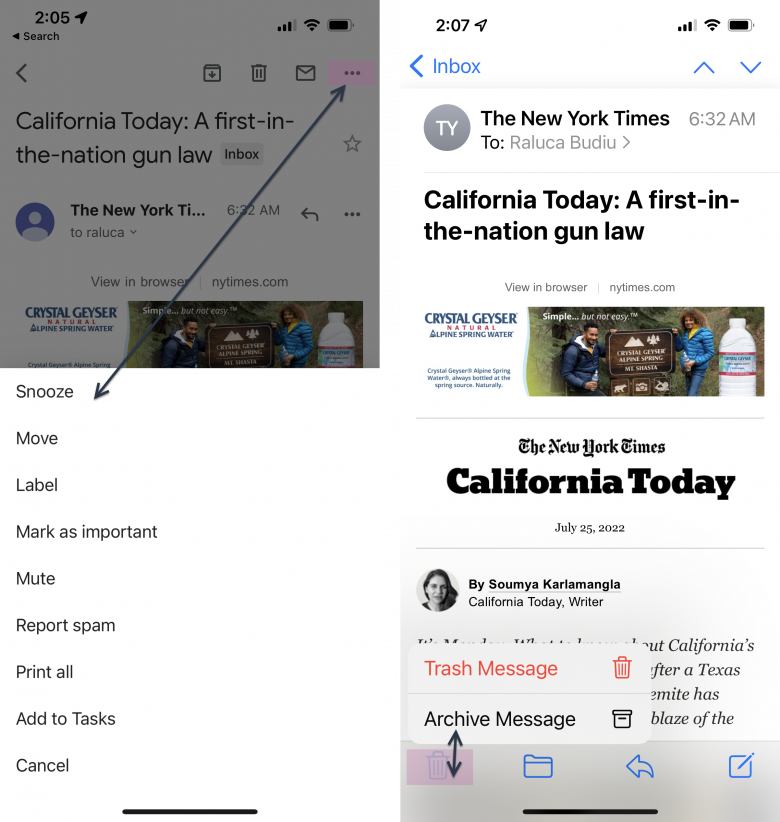
モバイルのコンテキストメニューには、メニューラベルから遠く離れた画面下部に出るシートに関連する選択肢を表示するものがある。このデザインはユーザーに移動時間を浪費させるので最適とはいえない。こうした選択肢はラベルの近くに表示されるのが理想だ。
関連するターゲット同士を近くに配置
一連のコントロール類が特定の順序でクリックされることがわかっている場合は、そのコントロール同士を近くに配置して(ただし、近すぎないようにする。上記のガイドラインを参照)、それらの間の距離を最小限に抑え、全体的なタスク時間を最適化するとよい。
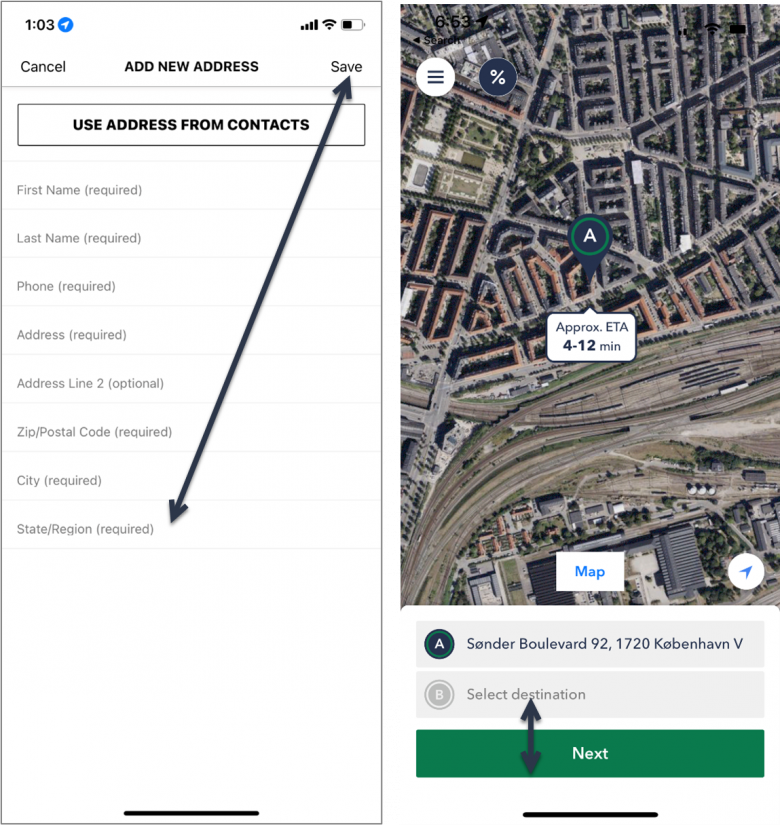
たとえば、フォームの「送信」ボタンは、最後の入力欄のすぐ近くに配置するべきだ。モバイルデザインで、「送信」ボタンをページの最上部、つまり、ページヘッダーに配置すると、上から下に見ていくというユーザーの自然なワークフローの流れに反するだけでなく、移動時間も最適化されない。画面の低い位置にある最後の入力欄から画面の最上部まで指を動かす必要があるからである。
結論
フィッツの法則によると、ターゲットまでの移動時間は、ターゲットの大きさとターゲットまでの距離に依存する。新たにUIをデザインするときは、2つの変数を最適化するために、十分な間隔で大きなターゲットを作成し、直前にユーザーのポインターがある可能性がもっとも高い場所の近くにそのターゲットを配置することを検討しよう。
参考文献
Avrahami, D. 2015. The Effect of Edge Targets on Touch Performance. CHI’15.
Elliott, D., Helsen, W. F., & Chua, R. (2001). A century later: Woodworth’s (1899) two-component model of goal-directed aiming. Psychological Bulletin, 127 (3), 342–357. https://doi.org/10.1037/0033-2909.127.3.342
Fitts, Paul M. (June 1954). “The information capacity of the human motor system in controlling the amplitude of movement”. Journal of Experimental Psychology. 47 (6): 381–391. https://doi.org/10.1037/h0055392
I. Scott MacKenzie and William Buxton. 1992. Extending Fitts’ law to two-dimensional tasks. In CHI ’92. New York, NY, USA, 219–226. https://doi.org/10.1145/142750.142794
記事で述べられている意見・見解は執筆者等のものであり、株式会社イードの公式な立場・方針を示すものではありません。