科学的法則とデザインの現場
Fittsの法則のような多くの心理学的な法則は、必ずしも実際の設計の現場でそれを利用するのが適切とは思われない。法則を適用する代わりに、実験を行って得たデータによって判断することが適切なのである。
この記事の目的
今回は、有名なFittsの法則を例として取り上げて、科学的法則というものとデザイン(設計)の現場との関係を考えてみたい。つまり、科学的法則を利用してデザインをやるべきなのかどうかということである。
心理学的な法則にはWeberの法則やFechnerの法則、ここで取り上げるFittsの法則、Hickの法則などたくさんのものがあるが、僕は、これらの法則は、科学的な目的で、人間の感覚系や知覚-運動系に関する現象を抽象化し、そこに見られる現象がランダムなものでなく、系統的なものであることを示すものであり、必ずしも工学的に応用するものではない、と思っている。
もちろん、Fechnerの法則は人間の感覚系を対数で表現できるものとして工学分野ではデシベル尺度を構成する根拠になっていたりする。しかし、多くの場合、そして特にここでとりあげるFittsの法則のような場合には、人間に見られる法則性を明らかにするという科学的目的のために構成されたものであり、必ずしも、実際の設計の現場でそれを利用するのが適切とは思われない。そのことをFittsの法則の説明から始めて論じてゆきたい。
Fittsの法則
この法則は、ひらたく言ってしまえば「指や手やスタイラス(棒)などで、ある位置をポイントする動作は、その位置までの距離が遠いほど長い時間がかかり、その位置のターゲットの大きさが小さいほど時間がかかる」というものである。
Ohio州立大学のFitts, P.Mは、1954年にJournal of Experimental Psychology誌に論文「The Information Capacity of the Human Motor System in Controlling the Amplitude of Movement」つまり「運動の大きさを調節する際の、人間の運動系の情報適応力」を発表した。
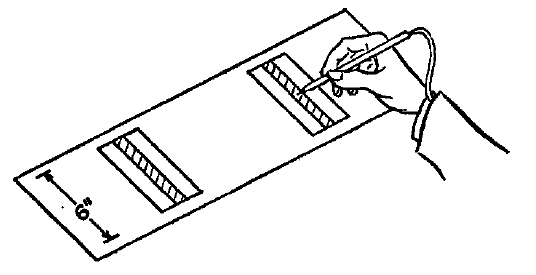
彼は3種類の装置を使って人間の運動系について実験を行った。最初の実験装置は下図のようなもので、奥行き6インチ(約15.2センチ)で目標エリア(図の斜線部分)の幅が2, 1, 0.5, 0.25インチ(約5.1, 2.5, 1.3, 0.6センチ)と異なっている4種類のボードである。二つの目標エリアの間の距離は、2, 4, 8, 16インチ(約5.1, 10.2, 20.3, 40.6センチ)となっており、目標エリアの幅と距離の組み合わせで、全部で16種類のパターンがあった。
右利きの男性被験者16人の右手にスタイラスを持たせ、スピードよりは正確さを重んじるように教示して、反対側の目標エリアに持って行き、それを元に戻す、という反復的な動作を行わせて、その所要時間を測定した。
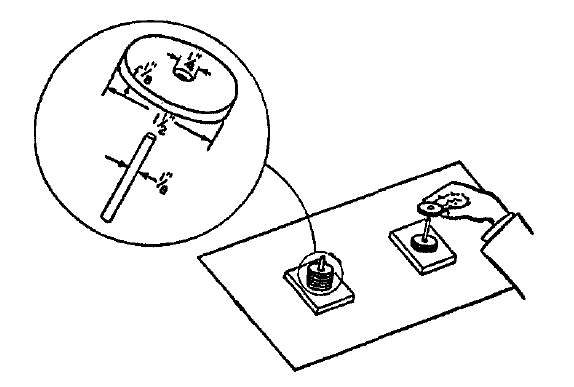
二番目の実験は下図のような装置で、直径1.5インチ(約3.8センチ)、厚さ1/8インチ(約0.3センチ)のプラスチックの8枚のワッシャー(穴のあいた円盤)を右の杭から左の杭に移動させるものだった。杭の太さとワッシャーの穴の比率は、1/2, 1/4, 1/8, 1/16であり、杭の間の距離は4, 8, 16, 32インチ(約10.2, 20.3, 40.6, 81.3センチ)で、ここでも合計で16種類の組み合わせが用意された。
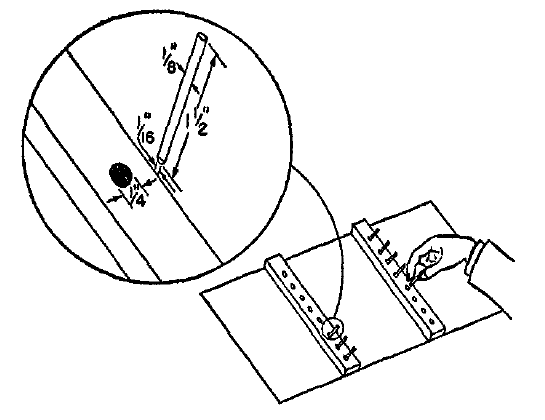
三番目の実験では、下図のように、8本のピンを1本ずつ移動する作業を行わせた。ピンの直径は、1/4, 1/8, 1/16, 1/32インチ(約0.6, 0.3, 0.2, 0.1センチ)で、移動距離は、1, 2, 4, 8, 16インチ(約2.5, 5.1, 10.2, 20.3, 40.6センチ)、合計で20の組み合わせができた。
つまり、いずれの実験でも、スタイラスや手を移動して、その移動距離と目標のサイズとを実験変数にしていたわけである。この実験データをもとにして、Fittsは情報分析的なモデルを提唱した。なお、当時、1950年代は、Shannon, C.E.などの情報理論や通信理論が華やかな時代であり、Fittsのモデルもその影響を受けてか、2を底とする対数を用いてモデル構築をしている。
彼が提示したモデルは、困難さの二値的な指標(Id)に関する
Id = – log2 D/2S bits/response(1)
というもの(Fittsは、距離についてWs、サイズについてAmplitudeの意味でAを使っていたが、本稿では後の研究者、たとえばCard, S.K.達(1986)のように距離のDとサイズのSとした)と、パフォーマンスの二値的な指標(Ip)についての
Ip = – 1/t log2 D/2S bits/sec(2)
というモデルである。tは所要時間である。
(2)式からわかるように、Fitts自身は、後年このモデルが活用されるようになった時間予測ではなく、あくまでも運動系の情報適応力の定式化を目指してモデル構築をしたのである。
Card等による紹介
Fittsの法則がHCI分野で有名になった背景には、Card,S.K., Moran, T.P. and Newell, A.の『The Psychology of Human Computer Interaction』(1986)で紹介されたことがある。この本でCard等は、下図を用いてFittsのオリジナルな実験を単純化している。
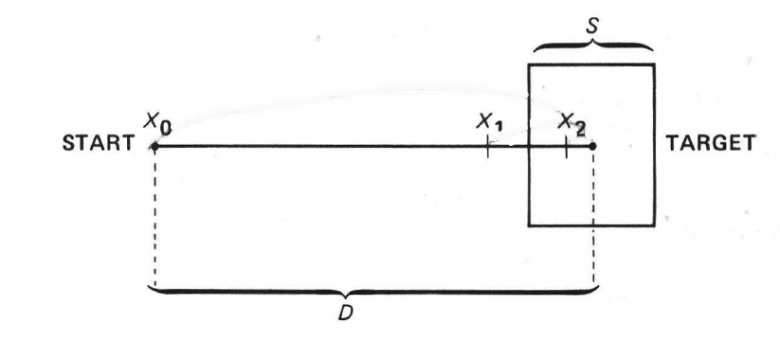
また、Fittsの法則を、時間予測のモデルとして書き直すために、さらに詳細な式の展開を行い、スタイラスや手が目標に到達するまでに行われているであろう逐次の方向修正をも考慮してεというパラメータを導入したりしている。その結果、
Tpos = – (τp+τC+τM) log2 (2D/S) / log2ε(3)
としている。ここでTposはポジショニングタイム、つまり所要時間、τp,τC,τMはそれぞれ知覚、修正、運動に要する時間、εはXi / X i-1 (ε<1)という逐次修正のパラメータである。それを単純化して得られる
Tpos = IM log2 (2D/S)(4)
という式としてFittsの法則を紹介している。なお、
IM = – (τp+τC+τM) / log2 ε
= – 240 msec / log2 (0.07) bits
= 63 msec / bit(5)
と具体的な数値にしている。ただし、これだとデータとの適応度が低いので、
IM = 100 [50~120] msec/bit(6)
と修正している。これにより
Tpos = 100 [50~120] log2 (2D/S) (msec / bit)(7)
という時間予測式が得られることになる。なお、さらに実験データへの適応度を高めるためにWelford, A.T.(1968)による変法を用いて
Tpos = IM log2(D/S + .5)(8)
としている。
今日、Fittsの法則として、(4)式と(8)式が混じって紹介されているのは、実験データへの適合度の問題であり、さほど重要な問題ではない。ただ、適合度が高いのは(8)の方、ということになる。
なお、Wikipediaには、つぎの(9)式のShannon-Hartleyの定理から援用した(10)式が紹介されている。
C = B log2 (1 + S/N)(9)
ここでCは通信路の容量(bit/sec)、Bは帯域幅(Hz)、SとNは信号とノイズの総電力、つまりS/NでいわゆるS/N比となる。
Tpos = a + b log2 (1 + D/S)(10)
ここでaは装置の開始・停止時間、bはデバイスの速度である。この形の導出についてはWikipediaを参照されたい。
インタフェースデザインにおける科学的法則の使い方
さて、本稿で本当に言いたいことはこれからである。まず、ポインティング操作に関する科学的法則は、(4)もしくは(8)、あるいは(10)のような形で定式化されたけれど、デザインの現場でこの法則を使うことはあるのか、ないのか、ということである。
工学という領域が科学的知見の応用である、という見方からすれば、ポインティング操作に関するデザインをする際には、まずFittsの法則を適用して予測値を得て、Tposの小さな方式を採用するようにすればよい、ともいえるのだが、もしかしてそれは迂遠なアプローチではないだろうか。
そこなのだ。科学的知見は科学としての精緻化において意義があり、人間のポインティング操作についてこのようなモデルが得られたことは「科学としては意義がある」。それは確かなことだ。しかし、実際のところ、その適合度には限界があり、Card達みずから、実験データに適合させるために式を修正しているではないか。要するに、一番信頼できるのは、きちんと条件設定されたうえでの実験データなのである。そして、インタフェースデザインの立場からすれば、それがどのような式として表現されようと、さしたる重要性はない、と言い切ってしまっていいだろう。
もちろん、工学のなかでは、実際に実験を行ううえで幾多の困難さがあり、まずは予測的なシミュレーションを行わねばならないケースはありうる。宇宙船の打ち上げなどでは、シミュレーションや予測計算が重要であり、とりあえずまず打ち上げてみようなどということはできない。しかし、ことインタフェースデザインに関して、実験的な検討に費用も時間も安全性も大きな問題になるようなケースがどれだけあるだろう。注意していただきたいが、ここでは、あくまでもインタフェースデザインについての話をしているのであって、原子炉や宇宙船の設計の話をしているわけではない。
だから、たとえば新しいポインティングデバイスを考えたとか、新しい操作パネルを考えたという場合、つまりFittsの法則が適用できるような場面に関しては、まず実験を行い、データを得て、それによって判断することが適切なのである。Fittsの法則を使う必要はないのだ。繰り返しになるが、数式的な予測が意味を持つのは、実験が、費用や時間、安全性などにおいて実験が困難な場合の話である。いいかえれば、Fittsの法則によって予測を行う必要性はデザインの現場ではまずない、と言ってもいいだろう。
デザインの現場における科学的法則の使い方については、より現実的な態度で臨むべきだろう。
補筆
こう書いて、一度は稿を閉じたのだけど、ひとこと注意書きをしておかないと誤解される恐れもあるかな、と考えて補筆する。
僕が書いたのはFittsの法則のような科学的法則を用いた予測がデザインの現場では意味がないということであり、Fittsの法則のような法則性を求めようとする科学的研究や工学的研究の意義を貶めようということではない。さらには、法則の適用に代えて実験をすべきことを推奨しているのであって、何もせずに直感で突き進めばいいと書いたわけではない。少なくとも諸法則についての基礎的な知識はもっておくべきだし、心理学的な実験のイロハは身につけておくべきだ。
実験による検証という実証的なスタンスを忘れてはいけないということは、デザイナー諸氏に対してしつこく強調しておきたい。
記事で述べられている意見・見解は執筆者等のものであり、株式会社イードの公式な立場・方針を示すものではありません。